Bilangan Berpangkat,Bentuk Akar, Soal dan Pembahasan

BAB 1.BILANGAN BERPANGKAT DAN BENTUK AKAR

Kata pengantar
Pengertian bilangan berpangkat
1. Pengertian bilangan berpangkat
2. jenis-jenis bilangan berpangkat
3. bilangan berpangkat positif
4. bilangan berpangkat negatif
5. jenispenjumlahanbilangan berpangkat
Soal–Soalbilangan berpangkat
Daftar pustaka

DAFTAR ISI

Daftar Isi………………………………………………………………………………………………………………………………………………………2

Bilangan Berpangkat……………………………………………………………………………………………………………………………………4

Jenis – jenis Bilangan Berpangkat……………………………………………………………………………………………………….…5

1. Bilangan Berpangkat Positif

2. Bilangan Berpangkat Negatif

3. Bilangan berpangkat Nol (0)

Sifat-sifat Bilangan Berpangkat…………………………………………………………………………………………………….………8

1. Pangkat Bulat positif

2. Pangkat Bulat Negatif

3. Pangkat Nol

4. Sifat-sifat Pangkat Bulat Positif

5. Pangkat Pecahan

Operasi Hitung Bilangan Berpangkat……………………………………………………………………………………………….……14

1. Sifat Perkalian Bilangan Berpangkat

2. Sifat Pembagian Bilangan Berpangkat

3. Sifat Perpangkatan Bilangan Berpangkat

4. Sifat Perpangkatan Suatu Perkalian Dua Bilangan

5. Sifat Perpangkatan Suatu Pembagian Dua Bilangan

6. Sifat Perpangkatan Bilangan nol

Contoh Soal………………………………………………………………………………………………………………………………………………..22

Daftar Pustaka……………………………………………………………………………………………………………………………………………33

1. Bilangan Berpangkat Sederhana

Dalam kehidupan sehari-hari kita sering menemui perkalian bilangan-bilangan dengan faktor-faktor yang sama. Misalkan kita temui perkalian bilangan-bilangan sebagai berikut.

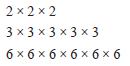
Perkalian bilangan-bilangan dengan faktor-faktor yang sama seperti di atas, disebut sebagai perkalian berulang. Setiap perkalian berulang dapat dituliskan secara ringkas dengan menggunakan notasi bilangan berpangkat. Perkalian bilanganbilangan di atas dapat kita tuliskan dengan:

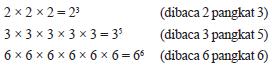
Bilangan 2³, 3⁵, 6⁶ disebut bilangan berpangkat sebenarnya karena bilangan-bilangan tersebut dapat dinyatakan dalam bentuk perkalian berulang. Bilangan berpangkat aⁿ dengan n bilangan bulat positif didefinisikan sebagai berikut.

2. Bilangan Berpangkat Negatif

Apa yang terjadi jika m = 0? Dari pembahasan di atas jika dipilih m = 0, maka:

B. Bilangan Pecahan Berpangkat

Untuk menentukan hasil pemangkatan bilangan pecahan berpangkat dapat di gunakan definisi bilangan berpangkat. Jika a, b∈ B, b ≠ 0, n adalah bilangan bulat positif maka:

C. Bentuk Akar

Dalam matematika kita mengenal berbagai jenis bilangan. Beberapa contoh jenis bilangan diantaranya adalah bilangan rasional dan irrasional. Bilangan rasional adalah bilangan yang dapat dinyatakan dalam bentuk , dengan m, n ∈ B dan n ≠ 0. Contoh bilangan rasional seperti: , 5, 3 dan seterusnya. Sedangkan bilangan irrasional adalah bilangan riil yang tidak dapat dinyatakan dalam bentuk , dengan m, n ∈ B dan n ≠ 0. Bilangan-bilangan seperti termasuk bilangan irrasional, karena hasil akar dari bilangan tersebut bukan merupakan bilangan rasional.

Bilangan-bilangan semacam itu disebut bentuk akar. Sehingga dapat disimpulkan bahwa bentuk akar adalah akar-akar dari suatu bilangan riil positif, yang hasilnya merupakan bilangan irrasional.

1. Operasi Hitung Bentuk Akar

Dua bilangan bentuk akar atau lebih dapat dijumlahkan, dikurangkan, maupun dikalikan.

a. Penjumlahan dan Pengurangan Bentuk Akar
Untuk memahami cara menjumlahkan dan mengurangkan bilangan-bilangan dalam bentuk akar, perhatikan contoh – contoh berikut.

Dari contoh di atas, maka untuk menjumlahkan dan mengurangkan bilangan-bilangan dalam bentuk akar dapat dirumuskan sebagai berikut. Untuk setiap a, b, dan c bilangan rasional positif, berlaku hubungan: