Berawal dari tugas matematika di sekolah oleh guru matemtika yang memberi tugas untuk mencari pola – pola bilangan matematika, maka pada kesempatan kali ini saya akan membagikan beberapa jenis pola bilangan matematika. Tanpa panjang lebar, langsung saja kita ke pembahasannya.
Pola bilangan ganjil
- Pola bilangan ganjil memiliki pola 1, 3, 5, 7, 9 ….
- Barisan bilangan ganjil adalah 1,3, 5, 7, 9, …
- Deret bilangan ganjil adalah 1 + 3 + 5 + 7 + 9 + ….
- Rumus mencari suku ke ke-n adalah Un = 2n – 1
- Rumus mencari jumlah n suku pertama adalah Sn = n2
- Berikut adalah gambar pola dari bilangan ganjil

Pola bilangan genap
- Pola bilangan genap adalah 2, 4, 6, 8, 10, …..
- Barisan bilangan genap adalah 2, 4, 6, 8, 10, ….
- Deret bilangan genap adalah 2 + 4 + 6 + 8 + 10 + …..
- Rumus untuk mencari suku ke-n adalah Un = 2n
- Rumus mencari jumlah n suku pertama adalah Sn = n2 + n
- Gambar pola bilangan genap adalah sebagai berikut

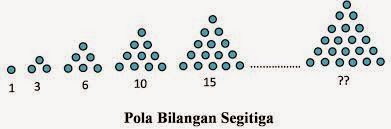
Pola bilangan segitiga
- Pola bilangan segitiga adalah 1, 3, 6, 10, 15, 21, …..
- Barisan bilangan segitiga adalah 1, 3, 6, 10, 15, 21, …..
- Deret bilangan segitiga adalah 1 + 3 + 6 + 10 + 15 + 21 + …..
- Rumus mencari suku ke-n adalah Un = ½ n (n + 1 )
- Rumus mencari jumlah n suku pertama adalah Sn = 1/6 n ( n + 1 ) ( n + 2 )
- Gambar pola bilangan segitiga adalah sebagai berikut
1PS2pKdSmpMHgLuCsLL52UwCtEgrG2_K_/
Pola bilangan persegi
- Pola bilangan persegi adalah 1, 4, 9, 16, 25, …..
- Barisan bilangan persegi adalah 1, 4, 9, 16, 25, …..
- Deret bilangan persegi adalah 1 + 4 + 9 + 16 + 25 + ……
- Rumus mencari suku ke-n adalah Un = n2
- Rumus mencari jumlah n suku pertama adalah Sn = 1/6 n ( n + 1 ) ( 2n + 1 )
- Gambar pola bilangan persegi adalah sebagai berikut

Pola bilangan persegi panjang
- Pola bilangan persegi panjang adalah 2, 6, 12, 20, 30, ……
- Barisan bilangan persegi panjang adalah 2, 6, 12, 20, 30, ……
- Deret bilangan persegi panjang adalah 2 + 6 + 12 + 20 + 30 + …..
- Rumus mencari suku ke-n adalah Un = n ( n + 1 )
- Rumus mencari jumlah n suku pertama adalah Sn = 1/3 n ( n + 1 ) ( n + 2 )
- Gambar pola bilangan persegi panjang adalah sebagai berikut

Pola bilangan segitiga pascal
- Rumus mencari jumlah baris ke-n adalah 2n – 1
- Gambar pola bilangan segitiga pascal adalah sebagai berikut


Pola bilangan Fibonacci
- Pola bilangan fibanocci adalah pola bilangan dimana jumlah bilangan setelahnya merupakan hasil dari penjumlahan dari dua bilangan sebelumnya.
- Pola bilangan Fibonacci adalah 1, 1, 2, 3, 5, 8, 13, 21, 34, …..
- 2 diperoleh dari hasil 1 + 1 3 diperoleh dari hasil 2 + 1, 5 diperoleh dari hasil 3 + 2 dan seterusnya
- Rumus mencari suku ke-n adalah Un = Un – 1 + Un - 2
Pola bilangan pangkat tiga
- Pola bilangan pangkat tiga adalah pola bilangan dimana bilangan setelahnya merupakan hasil dari pangkat tiga dari bilangan sebelumnya
- Contoh pola bilangan pangkat tiga adalah 2, 8, 512, 134217728, …..
- Keterangan : 8 diperoleh dari hasil 2 pangkat tiga, 512 diperoleh dari hasil 8 pangkat tiga, dan seterusnya
Pola bilangan aritmatika
- Pola bilangan aritmatika adalah pola bilangan dimana bilangan sebelum dan sesudahnya memiliki selisih yang sama.
- Contoh pola bilangan aritmatika adalah 2, 5, 8, 11, 14, 17, ….
- Suku pertama dalam bilangan aritmatika dapat disebut dengan awal ( a ) atau U1, sedangkan suku kedua adalah U2 dan seterusnya.
- Selisih dalam barisan aritmatika disebut dengan beda dan dilambangkan dengan b.
- Karena bilangan sebelum dan sesudahnya memiliki selisih yang sama, maka b = U2 - U1 = U3 – U2 = U4 – U3 = U5 – U4 = U6 – U5 = 3
- Rumus mencari suku ke-n adalah Un = a + ( n – 1 ) b
- Rumus mencari jumlah n suku pertama adalah Sn = n/2 ( a + Un ) atau Sn = n/2 ( 2 a + ( n – 1 ) b )
Saya rasa cukup sekian dulu tentang pola barisan bilangan yang dapat saya sampaikan kepada anda. Semoga dapat membantu anda dalam pelajaran matematika. Jangan lupa juga untuk update dari pola diatas, nanti setelah pegal – pegal saya hilang. Dan jangan lupa juga untuk LIKE FANSPAGE SPAKABAR DISINI untuk mendapatkan update dari blog ini melalui facebook.
Simak Juga : Pola Bilangan Barisan Dan deret
sumber: http://sapakabar.blogspot.com
