Persamaan Kuadrat, Pertidaksamaan, Fungsi Kuadrat

0

 

Baca Juga : Kumpulan Soal Persamaan Kuadrat SMP/Mts

Persamaan Kuadrat

Persamaan kuadrat adalah suatu persamaan dari variabel yang mempunyai pangkat tertinggi dua. Bentuk umumnya adalah:

ax^2 + bx + c = 0

Dengan a, b, merupakan koefisien, dan c adalah konstanta, serta a \neq 0 .

 

Penyelesaian atau pemecahan dari sebuah persamaan ini disebut sebagai akar-akar persamaan kuadrat. Akar-akar merupakan nilai dari variabel x yang memenuhi persamaan tersebut. Ketika nilai tersebut disubstitusikan ke dalam persamaan akan menghasilkan nilai nol.

Akar-akar Persamaan Kuadrat

Ada tiga metode dalam mencari akar-akar persamaan kuadrat ax^2 + bx + c = 0 yaitu:

Pemfaktoran

Metode ini mudah digunakan jika akar-akarnya merupakan bilangan rasional. Berikut ini tabel model persamaan kuadrat (PK) dan berbagai cara pemfaktorannya:

persamaan kuadrat dengan pemfaktoran

Saat menggunakan metode ini, pertama harus mengetahui terlebih dahulu model PK yang akan diselesaikan. Jika model PK sudah diketahui, maka pemfaktoran bisa dilakukan dalam bentuk sesuai dengan yang ada di kolom tabel di atas. Untuk mendapatkan nilai p, q, m dan n kalian harus memahami cara memfaktorkan suatu bilangan.

Melengkapkan Kuadrat Sempurna

Metode melengkapkan kuadrat sempurna akan mudah digunakan jika koefisien a dibuat agar bernilai 1. PK dalam bentuk ax^2 + bx + c = 0 diubah bentuk menjadi persamaan:

(x + p)^2 = q

Dengan p dan q adalah konstanta serta x adalah variabel. Nilai dari konstanta p dan q dari persamaan x^2 + bx + c = 0 didapatkan dengan cara:

p = \frac{1}{2}b

q = (\frac{1}{2}b)^2 - c

Perubahan tersebut dapat dibuktikan sebagai berikut :

(x + p)^2 = q

(x + \frac{1}{2}b)^2 = (\frac{1}{2}b)^2 - c

x^2 + bx + (\frac{1}{2}b)^2 = (\frac{1}{2}b)^2 - c

x^2 + bx + c = 0

Rumus abc

Metode rumus abc ini bisa digunakan jika pemfaktoran dan melengkapkan kuadrat sempurna tidak bisa dilakukan. Nilai dari akar-akar persamaan kuadrat ax^2 + bx + c = 0 didapatkan dari rumus abc berikut:

x_{1,2} = \frac{- b \pm \sqrt{b^2 - 4ac}}{2a}

Sehingga, akar-akarnya adalah

x_1 = \frac{- b + \sqrt{b^2 - 4ac}}{2a}

x_2 = \frac{-b - \sqrt{b^2 - 4ac}}{2a}

Jenis Akar-akar Persamaan Kuadrat

Jenis akar-akar persamaan kuadrat ax^2 + bx + c = 0 dapat ditentukan dengan mengetahui nilai “Diskriminan” (D). Nilai diskriminan terdapat dalam rumus abc sebagai :

D = b^2 - 4ac

Sehingga rumus abc menjadi:

x_{1,2} = \frac{-b \pm sqrt{D}}{2a}

Tanda akar diskriminan ( \sqrt{D} ) dalam rumus abc menentukan jenis dari akar-akar persaaman kuadrat, apakah bilangan real atau tidak real. Sehingga jenis akar-akar PK ax^2 + bx + c = 0 adalah:

  • Jika D < 0 maka akar-akarnya tidak real.
  • Jika D > 0 maka akar-akarnya real (x_1, x_2 \in R) dan berbeda (x_1 \neq x_2).
  • Jika D = 0 maka akar-akarnya real (x_1, x_2 \in R) dan sama atau kembar (x_1 = x_2).

Jumlah dan Hasil Kali Akar-akar

Penjumlahan dan perkalian akar-akar persamaan ax^2 + bx + c dapat dilakukan tanpa harus mengetahui nilai dari akar-akarnya. Jumlah akar-akar dapat diperoleh dengan :

x_1 + x_2 = \frac{-b + \sqrt{b^2 - 4ac}}{2a} + \frac{-b - \sqrt{b^2 - 4ac}}{2a}

= \frac{-b + \sqrt{b^2 - 4ac} - b - \sqrt{b^2 - 4ac}}{2a}

= - \frac{2b}{2a} = - \frac{b}{a}

Sedangkan hasil kali akar-akar dapat diperoleh dengan:

x_1 \cdot x_2 = \frac{-b + \sqrt{b^2 - 4ac}}{2a} \cdot \frac{-b -\sqrt{b^2 - 4ac}}{2a}

= \frac{(-b)^2 - (b^2 - 4ac)}{(2a)^2}

\frac{4ac}{4a^2} = \frac{c}{a}

Dari penjabaran tersebut dapat diketahui bahwa :

  • Penjumlahan akar-akar x_1 + x_2 = -\frac{b}{a}.
  • Perkailan akar-akar x_1 \cdot x_2 = \frac{c}{a}.

Ada beberapa bentuk pernyataan matematika yang bisa dirubah kedalam (x_1 + x_2) dan (x_1 \cdot x_2). Tujuan dari perubahan bentuk ini untuk memudahkan dalam peyelesaian persoalan. Perubahan ini dapat dilakukan dengan menggunakan sifat-sifat aljabar. Berikut ini sebagai contoh bentuk-bentuk perubahan:

  • x_1 + x_2 = (x_1 + x_2)^2 - 2x_1 \cdot x_2
  • x_1^3 + x_2^3 = (x_1 + x_2)^3 - 3 (x_1 \cdot x_2)(x_1 + x_2)
  • \frac{1}{x_1} + \frac{1}{x_2} = \frac{(x_1 + x_2)}{(x_1 \cdot x_2)}

Menyusun Persamaan Kuadrat Baru

Suatu persamaan kuadrat baru dapat dibentuk jika diketahui nilai dari akar-akarnya. Hal tersebut dapat dilakukan dengan memasukan atau mensubstitusi nilai dari akar-akar yang telah diketahui kedalam persamaan

(x - x_1)(x - x_2)

atau

x^2 - (x_1 + x_2)x + (x_1 . x_2)

Suatu persamaan kuadrat baru juga dapat dibentuk walaupun tidak ada diketahui nilai dari akar-akarnya. Dengan syarat, akar-akar tersebut memiliki hubungan atau relasi dengan akar-akar dari PK yang lain.

Contoh Soal Persamaan Kuadrat dan Pembahasan

Contoh Soal 1

Persamaan kuadrat dari x^2 - 4x - 6 = 0 mempunyai akar-akar m dan n dengan ketentuan m < n. Tentukan nilai dari n – m.

Pembahasan:

Soal ini dapat diselesaikan dengan cara melengkapkan kuadrat x^2 - 4x - 6 = 0 yang dirubah menjadi (x + p)^2. Dimana:

p = \frac{1}{2}b = \frac{1}{2}(-4) = -2

q = (\frac{1}{2}b)^2 - c = (\frac{1}{2}b)^2 - c

Kemudian disubstitusikan ke dalam persamaan

(x + p )^2 = q

(x - 2)^2 = 10

(x - 2) = \pm \sqrt{10}

x = 2 \pm \sqrt{10}

Didapatkan akar-akarnya dengan syarat m < n adalah

m = 2 - \sqrt{10}

n = 2 + \sqrt{10}

Maka,

n - m = 2 + \sqrt{10} - (2 - \sqrt{10})

= 2 + \sqrt{10}- 2 + \sqrt{10}

= 2\sqrt{10}

Contoh Soal 2

Suatu persamaan kuadrat x^2 - 2x - 5 = 0 memiliki akar-akar p dan q. Tentukan nilai dari (p^2 - q^2)^2.

Pembahasan :

Berdasarkan persamaan x^2 - 2x - 4 = 0 diketahui bahwa:

p + q = -\frac{b}{a} = -\frac{(-2)}{2} = 1

p . q = \frac{c}{a} = \frac{-4}{2} = -2

Sehingga diperoleh

(p^2 - q^2)^2 = ((p + q)(p - q))^2

= (p + q)^2 . (p - q)^2

= (p + q)^2 . (p^2 + q^2 - 2pq)

=(p + q)^2 . ((p + q)^2 - 2pq + 2pq)

= (1)^2 . ((1)^2 - 2(-2) - 2(-2))

= (1 + 4 + 4) = 9

Contoh Soal 3

Suatu persamaan kuadrat 2x^2 - 6x + 3 = 0 memiliki akar-akar p dan q. Tentukan persamaan kuadrat baru dengan akar-akar (p + q) dan (2pq).

Pembahasan :

Berdasarkan persamaan 2x^2 - 6x + 3 = 0 diketahui bahwa :

p + q = -\frac{b}{a} = -\frac{(-6)}{2} = 3

p \cdot q = \frac{c}{a}= \frac{3}{2} = 1,5

Sehingga akar-akar dari persamaan kuadrat baru adalah :

x_1 = (p + q) = 3

x_2 = 2pq = 2(1,5) = 3

Persamaan kuadrat baru diperoleh :

(x - x_1)(x - x_2)

(x - 3)(x - 3) atau x^2 - 6x + 9 = 0

Sumber: studiobelajar.com

PENERAPAN PERSAMAAN KUADRAT

Gerak suatu objek yang dilempar ke atas merupakan salah satu penerapan dari persamaan kuadrat dalam kehidupan sehari-hari. Gerak objek tersebut dapat dirumuskan dengan rumus h = –5t2 + vt + k, dengan h adalah ketinggian objek tersebut dalam meter, t adalah waktu dalam detik, dan v adalah kecepatan awal dalam meter per sekon. Konstanta k merepresentasikan ketinggian awal dari objek dari permukaan tanah. Untuk lebih memahami mengenai gerak objek yang dilempar ke atas, perhatikan contoh berikut.

Lihat Juga: Pertanyaan Seputar Office 365

Contoh 1: Menyelesaikan Penerapan Persamaan Kuadrat

Seorang anak berdiri di atas tebing yang memiliki ketinggian 5 m dari permukaan tanah, melempar bola ke atas dengan kecepatan awal 20 m/s (anggap bola dilepaskan ketika berada 1 m di atas permukaan tebing di mana anak tersebut berdiri). Tentukan (a) tinggi bola setelah 3 detik, dan (b) waktu yang dibutuhkan agar bola tersebut sampai di permukaan tanah.

Melempar Bola

Pembahasan Dengan menggunakan informasi yang diberikan soal, kita memperoleh h = –5t2 + 20t + 6. Untuk menentukan tinggi bola setelah 3 detik, substitusikan t = 3 ke dalam persamaan tersebut.

Menentukan Ketinggian

Apabila bola sampai di permukaan tanah, maka ketinggian bola tersebut adalah 0 meter. Sehingga dengan mensubstitusi h = 0 diperoleh,

Waktu Sampai Tanah

Karena waktu tidak pernah negatif, maka waktu yang diperlukan agar bola tersebut sampai di permukaan tanah adalah 4,28 detik.

Contoh 2: Permasalahan Pelanggan Telepon Genggam

Dari tahun 1995 sampai 2002, banyaknya pelanggan telepon genggam N (dalam juta orang) dapat dimodelkan oleh persamaan N = 17,4x2 + 36,1x + 83,3, dengan x = 0 merepresentasikan tahun 1995 [Sumber: Data dari 2005 Statistical Abstract of the United States, Tabel 1.372, hal. 870]. Pada tahun berapa banyaknya pelanggan telepon genggam mencapai angka 3.750 juta?

Pembahasan Dari soal diketahui bahwa N = 17,4x2 + 36,1x + 83,3 dan kita diminta untuk menentukan tahun ketika banyaknya pelanggan telepon genggam mencapai 3.750 juta. Dengan kata lain, kita diminta untuk menentukan nilai 1995 + x ketika N = 3.750.

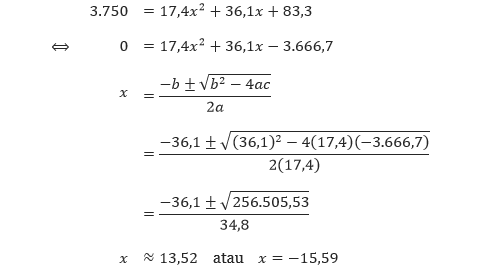
Pelanggan Telepon Genggam

Karena waktu tidak pernah negatif, maka kita simpulkan bahwa 13,52 tahun setelah tahun 1995, yaitu tahun 2008, banyaknya pelanggan telepon genggam mencapai angka 3.750 juta. Semoga bermanfaat.

SUMBER : https://yos3prens.wordpress.com

Rumus-rumus Persamaan Kuadrat

PERSAMAAN KUADRAT

Bentuk Umum Persamaan Kuadrat dalam x => ax2 + bx + c =o  (a,b,c  € R) dan a ≠ 0 
 
Cara menyelesaikan persamaan kuadrat ada 3, yaitu :
1. Memfaktorkan => (x-a) (x-b) = 0
    Contoh :
    a. X2 + 12x +32 = 0 => (x + 4) ( x + 8)
 
    b. X2  + x – 56   = 0 => (x + 8) (x – 7)
 
    c. X2 -6x – 27    = 0 => (x – 9) (x + 3)
 
    d. 2x2 – 5x – 3   = 0 => (2x – 1) (x + 3)
    e. 3x2 – 6x         = 0 => 3x(x – 2)
 
2. Melengkapi Kuadrat Sempurna => (x - p)2 = q
      Ada beberapa langkah, yaitu :
      1.  Koefisien x2 harus 1
      2. Konstanta pindah ke ruas kanan {-> x2 + mx = n
      3. Diubah ke bentuk kuadrat sempurna (x + p)2 = q
   
    Contoh :
    a. x2 + 8x + 12            = 0
        x2 + 8x                     = -12
        x2 + 8x + (1/2 . 8)2 = -12 + (1/2 . 8)2
        x2   + 8x + 16          = -12 + 16
               (x + 4)2             = 4
                x + 4                = ±√4
                      x                 = -4 ± 2

                      x                 = -6 , -2

3. RUMUS ABC => x1,2 = { -b ± √(b2 - 4ac) } / 2a
   Contoh :
    a. x2 + 8x + 5 => x1,2 = { -8 ± √(82 – 4.1.5) } / 2.1
                                          = { -8 ± √(64 – 20) } / 2

                                          = ( -8 ± √39 ) / 2

Penjumlahan dan Pekalian akar2 Penyelesaian Persamaan Kuadrat
dari x1,2 = { -b ± √(b2 - 4ac) } / 2a dengan D = b2 - 4ac maka x1 = (-b + √D) / 2a dan x2 = (-b - √D) / 2a
* D adalah Deskriminan

1. x1 + x2 = {(-b + √D) / 2a} + {(-b - √D) / 2a}
                    = (-b + √D - b - √D) / 2a
                    = -2b / 2a

                    = -b /a
Jadi, x1 + x2 = -b/a

2. x1 - x2 = {(-b + √D) / 2a} - {(-b - √D) / 2a}

                  = (-b + √D + b + √D) / 2a
                  = 2√D / 2a
                  = √D /a
Jadi, x1 - x2 = √D/a
 
3. x1 . x2 = {(-b + √D) / 2a} {(-b - √D) / 2a}
                  = (b2 - D) / 4a2
                  = b2 - (b2 - 4ac) / 4a2
                  = (b2 - b2 + 4ac) / 4a2
                  = 4ac / 4a2
                  = c/a

Jadi, x1 . x2 = c/a

4. (x1 + x2)2 = x12 + 2(x1 . x2) + x22
     (x1 + x2)2 - 2(x1 . x2) = x12 + x22
Jadi, x12 + x22 = (x1 + x2)2 - 2(x1 . x2)

5. (x1 + x2)3 = x13+ 3x12. x2 + 3x1 . x22 + x23
       (x1 + x2)3 -  3x12. x2 + 3x1 . x22 = x13 + x23 
              (x1 + x2)3 -  3x1.x2(x1 + x2)  = x13 + x23 
Jadi, x13 + x23 = (x1 + x2)3 -  3x1.x2(x1 + x2)

contoh soal!
1. Persamaan kuadrat -2x2 +4x-5=0 akar2nya α dan β
    Tentukan : a.  α + β                 d. α3 + β3
                        b. α . β                    e. 1/α + 1/β
                        c. α2 + β2                f. 1/(α+2) + 1/(β+2)
   Jawaban :
   a. α + β     = -b/a = 2
   b. α . β      = c/a   = 5/2
   c. α2 + β2 = (α + β)2 - 2(α . β)
                    = 22 - 2.5/2
                    = 4 - 5
                    = -1
   d. α3 + β3 = (α + β)3 - 3α.β (α+β )

   = 23  - 3.5/2.2

                    = 8 - 15
                    = -7
   e. 1/α + 1/β = (α + β) / αβ
                        = 2 / (5/2)
                        = 4/5
   f. 1/(α+2) + 1/(β+2) = {(α+2) + (β+2)} / {(α+2) (β+2)}
                                      = {(α+β) + 4} / {α.β + 2(α+β) + 4}
                                      = (2+4) / (5/2 + 2.2 + 4)
                                      = 6 / (21/2)
                                      = 12/21 

                                      = 4/7

Menyusun Persamaan Kuadrat Baru 
Ada 2 cara untuk menyusun persamaan kuadrat baru yang akar2nya x1 dan x2 yaitu,
1. (x - x1) (x - x2) = 0
Contoh soal : Susunlah Persamaan kuadrat baru yang akar2nya adalah
a. 2 dan 7 => PKB = (x - 2) (x -7)
                                  = x2 - 9x +14
b. -3 dan -4 => PKB = {x-(-3)} {x-(-4)}
                                    = (x+3) (x+4)
                                    = x2 + 7x + 12
c. -7 dan 2 => PKB = {x-(-7)} (x-2)
                                   = (x+7) (x-2)
                                   = x2 + 5x - 14
d. 5 dan -2 => PKB = (x-5) {x-(-2)}
                                   = (x-5) (x+2)
                                   = x2 - 3x - 10
 
2. x2 - (x1 + x2)x + x1.x2 = 0
 Contoh soal : 
1. Susunlah Persamaan Kuadrat baru yang akar2nya adalah 2+√5 dan 2-√5!
    Jawaban :  x1 + x2 = (2+√5) +(2-√5) = 4 
                            x1.x2 = (2+√5) (2-√5)  = -1
    Jadi, PKB => x2 - (x1 + x2)x + x1.x2 = 0

                       =>                    x2 - 4x - 1 = 0

2. x1 dan x2 adalah akar2 persamaan kuadrat  x2 - 2x + 5 = 0. Susunlah persamaan kuadrat baru yang akar2nya 3 lebihnya dari akar2 persamaan kuadrat yang diletahui.
Jawaban  : x1 + x2 = -b/a = 2 dan x1.x2 = c/a = 5
                     x1 = (x1 + 3) dan x2 = (x2 + 3)
maka, x1 + x2 = (x1 + 3) + (x2 + 3)                  dan             x1.x2 = (x1 + 3) (x2 + 3)     
                         = (x1 + x2) + 6                                                       = x1.x2 + 3(x1+x2) + 9
                         = 2 + 6                                                                   = 5 + 3.2 + 9
                         = 8                                                                          = 20
Jadi, PKB => x2 - (x1 + x2)x + x1.x2 = 0

                    =>                x2 - 8x + 20 = 0

                    * Deskriminan (D) => D = b2 - 4ac *
 
untuk menentukan jenis akar2 persamaan kuadrat, rumusnya :
a. D = 0 => Mempunyai 2 akar yang sama
b. D < 0 => Tidak mempunyai akar nyata (akar2nya imajiner)
c. D ≥ 0 => Mempunyai 2 akar nyata
d . D > 0 => Mempunyai 2 akar nyata dan berlawanan
 
Contoh Soal :
1. Tentukan nilai k agar persamaan kuadrat kx2 + 3x + k = 0 mempunyai 2 akar sama/kembar
    Jawaban : Syarat akar kembar D = 0, maka
                        b2 - 4ac = 32 - 4.k.k
                                     0 = 9 - 4k2
                                 4k2 = 9
                                     k = √(9/4)
                        k = ± 3/2
 
2. Tentukan m agar persamaan kuadrat berikut x2 - 2x + (m+1) = 0 Tidak mempunyai akar nyata.
     Jawaban : Syarat tidak mempunyai akar nyata D < 0, maka
                                 b2 - 4ac < 0
                       22 - 4.1.(m+1) < 0
                               4 - 4m - 4 < 0
                                    0 - 4m < 0
                                       - 4m < 0
                                            m > 0
 
3. Tentukan P agar persamaan kuadrat x2 + px + p = 0 mempunyai 2 akar real dan berbeda.
     Jawaban : Syarat akar real dan berbeda D > 0, maka
                             b2 - 4ac > 0
                           p2 - 4.1.p > 0
                               p2 - 4p > 0
                              p(p - 4) > 0 
    Jadi, p < 0 dan p > 4 

You may like these posts

Post a Comment

pardomuansitanggang@gmail.com

Previous Post Next Post